The Mathematical Breakdown: 117 Divided By 26 Explained

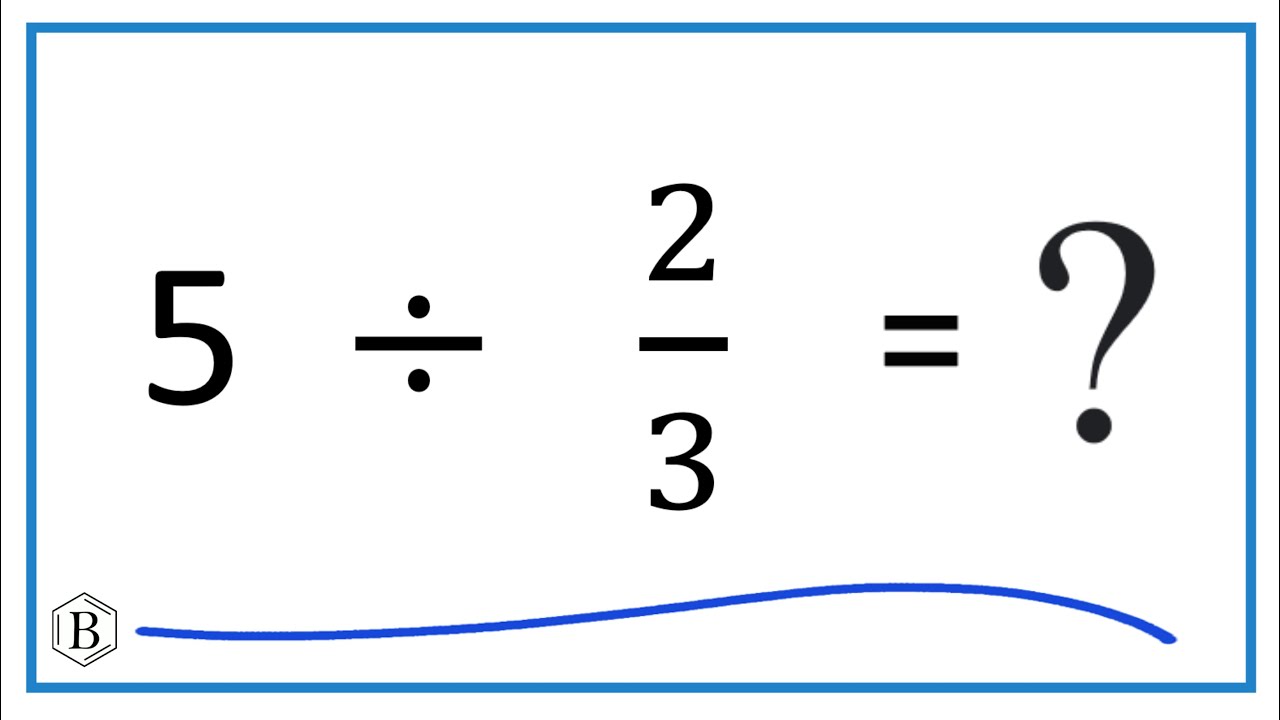
In the realm of mathematics, division serves as a fundamental operation, allowing us to distribute a quantity into equal parts or groups. When faced with the division of 117 by 26, one might wonder about the significance and applications of this calculation. Understanding the division of numbers is crucial, not only for academic purposes but also for practical applications in daily life. This article delves into the specifics of dividing 117 by 26, uncovering the nuances and implications of this mathematical operation.

Division is a math operation that essentially asks how many times one number is contained within another. In the case of 117 divided by 26, it prompts us to consider how many times 26 can be subtracted from 117 before reaching zero. This calculation is not just an arithmetic exercise; it offers insights into proportionality, fractions, and real-world problem-solving. As we explore this mathematical process, we'll gain a deeper appreciation for the logic and reasoning behind division.

While the equation 117 divided by 26 may initially appear straightforward, it holds layers of complexity and meaning. This article will explore various methods to solve this division, interpret the result, and apply it in different contexts, making the seemingly simple question an engaging journey through the world of numbers. As we navigate through the following sections, our aim is to not only solve the equation but to illuminate the broader mathematical concepts it represents.

Table of Contents

• Understanding Division
• The Process of Dividing 117 by 26
• Why is Division Important in Mathematics?
• Real-World Applications of Dividing 117 by 26
• How Do We Interpret the Result of 117 Divided by 26?
• Division in Different Number Systems
• Historical Perspective on Division
• Common Mistakes When Dividing Numbers
• Enhancing Division Skills
• How Can Technology Assist in Division?
• Educational Tools for Learning Division
• Advanced Concepts Related to Division
• What Are the FAQs About Division?
• Conclusion

Understanding Division

Division is one of the four basic operations of arithmetic, alongside addition, subtraction, and multiplication. It is the process by which a number (the dividend) is divided by another number (the divisor) to produce a result known as the quotient. In mathematical notation, the division of 117 by 26 is represented as 117 ÷ 26 or 117/26. Understanding the principles of division is essential for solving complex mathematical problems and for performing calculations in everyday life.

At its core, division asks how many times one number can be subtracted from another. It is the inverse operation of multiplication. For instance, if you multiply the quotient by the divisor, you should get the original dividend. This relationship highlights the interconnectedness of arithmetic operations and emphasizes the importance of mastering division.

Division can be executed through various methods, including long division, short division, and mental math. Each method has its advantages and is suitable for different contexts. Long division, for instance, provides a structured approach that is ideal for larger numbers, while mental math encourages quick and efficient calculations for simpler problems.

The Process of Dividing 117 by 26

Let's delve into the process of dividing 117 by 26 using the long division method. This technique involves several steps that systematically break down the division problem to arrive at an accurate quotient and remainder.

1. Set up the division problem: Write 117 under the division bar and 26 outside, to the left.
2. Estimate how many times 26 fits into 117: Begin by determining how many times 26 can be subtracted from the first digit or set of digits of 117. In this case, 26 goes into 117 four times.
3. Multiply and subtract: Multiply the quotient (4) by the divisor (26), resulting in 104. Subtract 104 from 117, leaving a remainder of 13.
4. Interpreting the result: The quotient is 4, with a remainder of 13. This means that 26 fits into 117 four times, with 13 left over. The division can also be expressed as 4 R13 or as a mixed number: 4 13/26.

Understanding the result of this division involves recognizing the significance of both the quotient and the remainder. The quotient represents the number of complete groups of 26 that can be formed from 117, while the remainder indicates the portion of 117 that cannot be evenly divided by 26.

Why is Division Important in Mathematics?

Division plays a critical role in mathematics and is foundational to many advanced concepts. It is essential for solving equations, performing calculus operations, and analyzing data. Division is used to find ratios, proportions, and averages, which are vital for making comparisons and informed decisions.

In academic settings, division is a key component of the mathematics curriculum and is tested in standardized assessments. Proficiency in division is necessary for success in mathematics and related fields, such as science, engineering, and economics. Division skills are also crucial for everyday activities, such as cooking, budgeting, and measuring.

Moreover, division is integral to understanding fractions, percentages, and decimals. These concepts are ubiquitous in both academic and real-world contexts, emphasizing the importance of mastering division to navigate various mathematical challenges.

Real-World Applications of Dividing 117 by 26

The division of 117 by 26 may appear abstract, but it has practical applications in various real-world scenarios. Understanding and applying this division can aid in problem-solving and decision-making in everyday life.

• Budgeting and finance: Division is essential for calculating expenses and distributing funds evenly. For example, if you have $117 and need to allocate it to 26 different expenses, dividing 117 by 26 will help determine the amount allocated to each expense.
• Time management: Division can help break down tasks or time periods into manageable segments. If you have 117 minutes to complete a project and want to divide it into 26 equal intervals, dividing 117 by 26 provides the duration of each interval.
• Cooking and recipes: Division is often used in scaling recipes to serve a different number of people. If a recipe requires 117 grams of an ingredient and you need to adjust it for 26 servings, dividing 117 by 26 determines the amount needed per serving.

These examples highlight the versatility and utility of division in daily life, reinforcing the value of understanding and applying division in diverse contexts.

How Do We Interpret the Result of 117 Divided by 26?

Interpreting the result of 117 divided by 26 involves recognizing the significance of both the quotient and the remainder. The quotient represents the number of complete groups of 26 that can be formed from 117, while the remainder indicates the portion of 117 that cannot be evenly divided by 26.

In practical terms, the quotient (4) signifies that 26 can be subtracted from 117 a total of four times, leaving a remainder of 13. This remainder can be expressed as a fraction (13/26), which simplifies to 1/2. Thus, the division of 117 by 26 can also be represented as a mixed number: 4 1/2.

This interpretation is valuable for understanding proportionality and fractions. Recognizing that 117 is equivalent to 4 times 26 plus 13 helps contextualize the division, facilitating the application of this concept in various mathematical and real-world scenarios.

Division in Different Number Systems

Division is not limited to the decimal number system; it can be performed in various number systems, such as binary, octal, and hexadecimal. Each system has its own base and symbols, influencing the division process and interpretation of results.

In the binary system (base 2), division involves breaking down numbers into powers of 2. In this system, 117 is represented as 1110101, and 26 is represented as 11010. Dividing these binary numbers follows the same principles as decimal division, but with binary arithmetic rules.

The octal system (base 8) and hexadecimal system (base 16) operate similarly, using their respective bases and symbols. Understanding division in these systems is crucial for computer science and digital electronics, where binary and hexadecimal numbers are prevalent.

Historical Perspective on Division

Division has a rich history dating back to ancient civilizations. Early mathematicians developed methods for division to solve practical problems, such as distributing resources and calculating trade values.

The Babylonians, Egyptians, and Greeks all contributed to the development of division techniques. The Babylonians used tables of reciprocals to perform division, while the Egyptians employed a method known as "duplation" or "halving." The Greeks refined these techniques and laid the groundwork for modern arithmetic.

Over time, division evolved into a more formalized mathematical operation, with the introduction of symbols and rules that are still used today. The development of algebra and calculus further advanced the understanding and application of division in mathematics.

Common Mistakes When Dividing Numbers

Despite its simplicity, division can be challenging and prone to errors. Common mistakes include misinterpreting the divisor and dividend, incorrectly estimating the quotient, and failing to account for remainders.

• Misaligning numbers: Ensure that numbers are properly aligned during long division to avoid calculation errors.
• Incorrect estimation: Carefully estimate the quotient to prevent overshooting or undershooting the correct result.
• Neglecting remainders: Always consider the remainder in division problems, as it affects the final result and interpretation.

Being mindful of these common pitfalls can help improve accuracy and confidence when performing division calculations.

Enhancing Division Skills

Improving division skills requires practice, understanding, and the application of effective strategies. Here are some tips to enhance your division abilities:

• Practice regularly: Consistent practice with a variety of division problems helps reinforce concepts and build confidence.
• Use visual aids: Visualizing division through diagrams or models can aid comprehension and retention.
• Break down complex problems: Divide larger problems into smaller, more manageable parts to simplify calculations.

By adopting these strategies, learners can develop a stronger grasp of division and improve their mathematical proficiency.

How Can Technology Assist in Division?

Technology offers numerous tools and resources to aid in teaching and learning division. Calculators, educational software, and online platforms provide interactive and engaging ways to explore division concepts.

Calculators allow for quick and accurate division calculations, enabling users to verify their work and explore more complex problems. Educational software offers interactive lessons and exercises that reinforce division skills through practice and feedback.

Online platforms provide access to tutorials, videos, and games that make learning division enjoyable and accessible. These resources cater to various learning styles and levels, supporting students in their mathematical journey.

Educational Tools for Learning Division

In the digital age, a wide array of educational tools are available to support division learning. These tools cater to different learning preferences and offer engaging ways to master division skills.

• Math apps: Mobile apps offer interactive division exercises that promote practice and understanding. Many apps include features like quizzes, challenges, and progress tracking.
• Online courses: Comprehensive online courses provide structured division lessons, covering basic to advanced concepts. These courses often include videos, worksheets, and assessments.
• Educational games: Gamified learning experiences make division fun and motivating. Games challenge students to solve division problems in creative and competitive ways.

By leveraging these educational tools, learners can enhance their division skills and gain confidence in their mathematical abilities.

Advanced Concepts Related to Division

As students progress in their mathematical journey, they encounter advanced concepts related to division. These concepts build on foundational division skills and introduce new challenges and opportunities for exploration.

• Long division with polynomials: This technique extends division to algebraic expressions, requiring students to divide polynomials by other polynomials.
• Division of complex numbers: Complex numbers, which include both real and imaginary components, present unique division challenges that involve understanding magnitude and phase.
• Division in calculus: Calculus introduces division in the context of derivatives and integrals, requiring a deep understanding of limits and infinitesimals.

Mastering these advanced concepts expands students' mathematical knowledge and prepares them for higher-level coursework and problem-solving.

What Are the FAQs About Division?

1. What is the difference between a quotient and a remainder?

The quotient is the result of a division problem, representing the number of times the divisor fits into the dividend. The remainder is the part of the dividend that is left over after division.

2. How can I improve my division skills?

Practice regularly, use visual aids, break down complex problems, and leverage technology and educational tools to enhance your division skills.

3. Why is division important in real life?

Division is essential for tasks such as budgeting, time management, cooking, and problem-solving, making it a valuable skill in everyday life.

4. What are some common mistakes when dividing numbers?

Common mistakes include misaligning numbers, incorrect estimation, and neglecting remainders. Being mindful of these errors can improve accuracy.

5. How does division relate to fractions?

Division is closely related to fractions, as it represents the process of splitting a whole into parts. Understanding division helps in interpreting and working with fractions.

6. Can division be performed in different number systems?

Yes, division can be performed in various number systems, such as binary, octal, and hexadecimal, each with its own rules and symbols.

Conclusion

The division of 117 by 26 offers a fascinating glimpse into the world of mathematics, revealing the intricate processes and concepts underlying this fundamental operation. By understanding and mastering division, learners can unlock new mathematical horizons and apply their skills in practical, real-world contexts. Whether through traditional methods or modern technology, the journey of exploring division is both enlightening and empowering, paving the way for continued growth and discovery in the realm of numbers.